Intuition Behind the Attention Head of Transformers
Even as I frequently use transformers for NLP projects, I have struggled with the intuition behind the multi-head attention mechanism outlined in the paper - Attention Is All You Need. This post will act as a memo for my future self.
Limitation of only using word embeddings
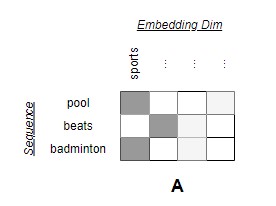
Consider the sequence of words - pool beats badminton. For the purpose of machine learning tasks, we can use word embeddings to represent each of them. The representation can be a matrix of three word embeddings.
If we take a closer look, the word pool has multiple meanings. It can mean a swimming pool, some cue sports or a collection of things such as money. Humans can easily perceive the correct interpretation because of the word badminton. However, the word embedding of pool includes all the possible interpretations learnt from the training corpus.
Can we add more context to the embedding representing pool? Optimally, we want it to be “aware” of the word badminton more than the word beats.
My intuition behind the self-attention mechanism
Consider that matrix A represents the sequence - pool beats badminton. There are three words (rows) and the word embedding has four dimensions (columns). The first dimension represents the concept of sports. Naturally, we expect the words pool and badminton to have more similarity in this dimension.
Diagram by Author
1
2
3
4
5
A = np.array([
[0.5, 0.1, 0.1, 0.2],
[0.1, 0.5, 0.2, 0.1],
[0.5, 0.1, 0.2, 0.1],
])
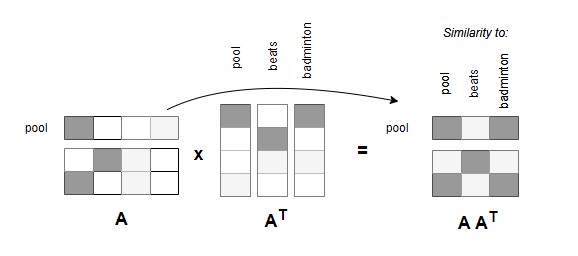
If we do a matrix multiplication between A and AT, the resulting matrix will be the dot-product similarities between all possible pairs of words. For example, the word pool is more similar to badminton than the word beats. In other words, this matrix hints that the word badminton should be more important than the word beats when adding more context to the word embedding of pool.
Diagram by Author
1
2
3
4
5
A_At = np.matmul(A, A.T)
>>> A_At
array([[0.31, 0.14, 0.3 ],
[0.14, 0.31, 0.15],
[0.3 , 0.15, 0.31]])
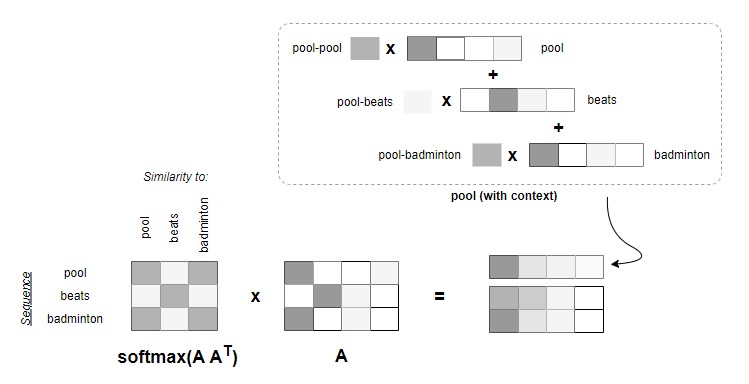
By applying the softmax function across each word, we can ensure that these “similarity scores” add up to 1.0.
The last step is to do another matrix multiplication with matrix A. In a way, this step consolidates the contexts of the entire sequence to each embedding in an “intelligent” manner. In the example below, both embeddings of beats and badminton are added to pool but with different weights depending on their similarities with pool.
Diagram by Author
1
2
3
4
5
6
7
output = np.round(
np.matmul(softmax(A_At, axis=1), A)
, 2)
>>> output
array([[0.38, 0.22, 0.16, 0.14],
[0.35, 0.25, 0.17, 0.13],
[0.38, 0.22, 0.17, 0.13]])
Notice that the output matrix has the same dimensions (3 x 4) as the original input A. The intuition is that each word vector is now enriched with more information. This is the gist of the self-attention mechanism.
Scaled Dot-Product Attention
The picture below shows the Scaled Dot-Product Attention from the paper. The core operations are the same as the example we explored. Notice that scaling is added before softmax to ensure stable gradients, and there is an optional masking operation. Inputs are also termed as Q, K and V.
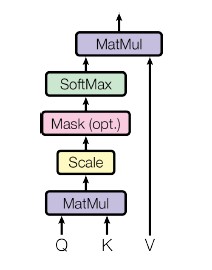Image taken from Attention Is All You Need paper
The Scaled Dot-Product Attention can be represented as attention(Q, K, V) function.
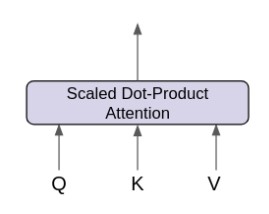Diagram by Frank Odom on Medium
Adding trainable weights with linear layers
The initial example that we use can be represented as attention(A, A, A), where matrix A contains the word embeddings of pool, beats and badminton. So far there are no weights involved. We can make a simple adjustment to add trainable parameters.
Imagine we have (m x m) matrices MQ, MK and MV where m matches the dimension of word embeddings in A. Instead of passing matrix A directly to the function, we can calculate Q = A MQ, K = A MK and V = A MV which will be the same sizes as A. Then we apply attention(Q, K, V) afterwards. In neural network, this is akin to adding a linear layer before each input into the Scaled Dot-Product Attention.
To complete the Single-Head Attention mechanism, we just need to add another linear layer after the output from the Scaled Dot-Product Attention. The idea of expanding to the Multi-Head Attention in the paper is relatively simpler to grasp.
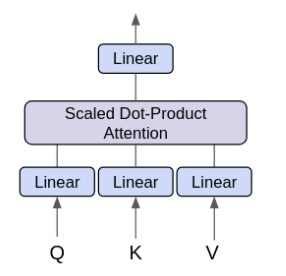Diagram by Frank Odom on Medium