Speed up Python applications With Ctypes Library
There are multiple ways to speed up computations in Python. The cython language compiles Python-like syntax into CPython extensions. Libraries such as numpy provides methods to manipulate large arrays and matrices efficiently with underlying C data structures.
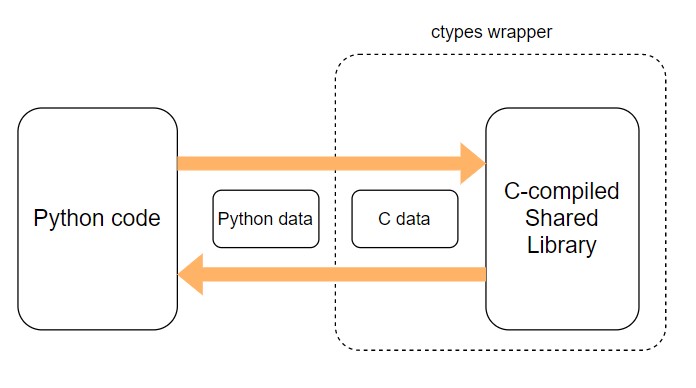
In this post, I will be discussing the ctypes module. It provides C-compatible data types to so that Python functions can use C-compiled shared libraries. Therefore, we can offload computationally intensive modules of a Python application into C where the developers will have more fine-grained control. To my surprise, this comes as part of the Python standard library, so no external dependencies are required!
Code to optimize - prime number checker
I have created a sample program that we can speed up afterwards using the ctypes module. The num_primes() calculates the total number of primes in a list by looping through each item.
1
2
3
4
5
6
7
8
9
10
11
12
# prime.py
def is_prime(num: int):
for i in range(2, int(num**(0.5))):
if num % i == 0:
return 1
return 0
def num_primes(num_list: List[int]):
count = 0
for num in num_list:
count += is_prime(num)
return count
Let’s see the number of primes in a list of 1 million integers. Note that we use consecutive numbers for the example but it does not have to be.
1
2
3
4
5
6
7
8
9
from prime import num_primes
MAX_NUM = 1000000
num_list = list(range(MAX_NUM))
def timeit_function():
return num_primes(num_list)
print(timeit_function())
It takes around 3.4 seconds to run. How can we speed this up?
1
2
3
>>> python -m timeit -n 5 -s 'import test_python as t' 't.timeit_function()'
Primes: 921295
5 loops, best of 5: 3.4 sec per loop
Why Python threading module does not work
As Python has a threading module, one idea is to parallalize calculations across the entire list by using multiple threads. However, this is not possible due to Python’s Global Interpreter Lock (GIL), which prevents multiple threads in a process from executing Python bytecode at the same time. Hence for non-I/O operations, there will not be any speed up.
Rewriting prime checker in C
The prime checker is reimplemented in C as shown below, then compiled it into a shared library prime.so. Note that the program logic is exactly the same.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// prime.c
#include <stdio.h>
#include <math.h>
int is_prime(int num) {
for (int i=2; i<(int)sqrt(num); i++) {
if (num % i == 0)
return 1;
}
return 0;
}
int num_primes(int arrSize, int *numArr) {
int count = 0;
for (int i=0; i<arrSize; i++)
count += is_prime(numArr[i]);
return count;
}
Calling the C-compiled prime checker with ctypes
The ctypes library provides C-compatible data types in Python. All we need to do is load the shared library with CDLL() API and then declare the parameters/ return types accordingly with argtypes and restype attributes.
1
2
3
4
5
6
7
8
from ctypes import *
# Load the shared library
lib = CDLL("./libprime.so")
# Declare the return data as 32-bit int
lib.num_primes.restype = c_int32
# Declare the arguments as a 32-bit int and a pointer for 32-bit int (for list)
lib.num_primes.argtypes = [c_int32, POINTER(c_int32)]
Afterwards, the num_primes() in the shared library can be called! Note that the num_list has to be converted from Python list into a contiguous array of C with a method provided by ctypes.
1
2
3
4
5
6
7
8
MAX_NUM = 1000000
num_list = list(range(MAX_NUM))
def timeit_function():
# num_list is converted into an integer array of size MAX_NUM
return lib.num_primes(MAX_NUM, (c_int32 * MAX_NUM)(*num_list))
print(f"Primes: {timeit_function()}")
For the same input of 1 million integers, the speed up is significant just by offloading the same program logic to C code. It makes sense because contiguous arrays in C can leverage caching mechanisms better than lists in Python.
1
2
3
>>> python -m timeit -n 5 -s 'import test_ctypes as t' 't.timeit_function()'
Primes: 921295
5 loops, best of 5: 482 msec per loop
Multithreading in the C shared library with POSIX pthreads
There is one more benefit of offloading the work to C. Since the shared library is not under Python’s GIL, we can now use multithreading in C to parallelize the computations!
In the code below, the integer array is split evenly into 4 subarrays and 4 threads are spawned with POSIX pthreads to do parallel work. Each thread runs thread_function() to check the numbers in the array without any overlap between threads. The counts of prime numbers are added into countByThreads array which are summed up after the child threads have terminated.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#define NUM_THREADS 4 // 4 threads used
// Global variables for spawn threads to access
int *gArrSize = 0; // Ptr for array size
int *gNumArr = 0; // Ptr for input array
int countByThreads[NUM_THREADS] = { 0 }; // Prime counts of each thread
pthread_t tids[NUM_THREADS] = { 0 }; // IDs of each thread
// Function run by each thread
void *thread_function(void *vargp) {
// Each thread has a different offset
int offset = (*(int*) vargp);
int count = 0;
// Split the array items evenly across threads
for (int i=offset; i < *gArrSize; i+=NUM_THREADS)
count += is_prime(gNumArr[i]);
countByThreads[offset] += count;
free(vargp);
}
int num_primes(int arrSize, int *numArr) {
gArrSize = &arrSize;
gNumArr = numArr;
for(int i=0; i < NUM_THREADS; i++) {
int *offset = (int*) malloc(sizeof(int));
*offset = i;
if(pthread_create(&tids[i], NULL, thread_function, (void *) offset) == -1)
exit(1);
}
int count = 0;
for(int i=0; i < NUM_THREADS; i++) {
if(pthread_join(tids[i], NULL) == -1)
exit(1);
// Combine counts from each thread after termination
count += countByThreads[i];
countByThreads[i] = 0;
}
return count;
}
We have further sped up the code execution although there is an additional overhead of managing threads.
1
2
3
>>> python -m timeit -n 5 -s 'import test_ctypes_pthread as t' 't.timeit_function()'
Primes: 921295
5 loops, best of 5: 322 msec per loop
Calling the C-compiled prime checker with Python threading
Remember the threading module in Python just now? Another neat thing about ctypes is that the program releases the GIL as long as the execution is inside the C-compiled shared library. So instead of POSIX pthreads in C, we can generate the threads with threading instead!
1
2
3
4
5
6
7
8
from ctypes import *
# Load the shared library
lib = CDLL("./libprime.so")
# Declare the return data as 32-bit integer
lib.num_primes.restype = c_int32
# Declare the arguments as a 32-bit integer & a pointer for 32-bit integer (for list)
lib.num_primes.argtypes = [c_int32, POINTER(c_int32)]
Afterwards, the num_primes() in the shared library can be called! Note that the num_list has to be converted from Python list into a contiguous array with a method provided by ctypes.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
MAX_NUM = 1000000
NUM_THREADS = 4
# Prime counts per thread
count_list = [0 for _ in range(NUM_THREADS)]
# One list of numbers for each thread
num_list_list = []
# Split the list for multiple threads
for i in range(NUM_THREADS):
num_list = list(range(i, MAX_NUM, NUM_THREADS))
num_list_list.append(num_list)
# Function run by each thread
def thread_function(i, num_list, count_list):
len_num_list = len(num_list)
count_list[i] = lib.num_primes(len_num_list, (c_int32 * len_num_list)(*num_list))
def timeit_function():
threads = []
for i in range(NUM_THREADS):
t = threading.Thread(target=thread_function, args=(i, num_list_list[i], count_list))
t.start()
threads.append(t)
for thread in threads:
thread.join()
return sum(count_list) # Combine counts from each thread
print(f"Primes: {timeit_function()}")
For this example, the speed up is comparable to using pthreads.
1
2
3
>>> python -m timeit -n 5 -s 'import test_ctypes_threading as t' 't.timeit_function()'
Primes: 921295
5 loops, best of 5: 313 msec per loop
The code demonstrations can be found here.